Under What Circumstances Is the Definitional Formula Easy to Use

Psychology 240 Lectures
Chapter 4
Statistics one

Illinois State University
J. Cooper Cutting
Fall 1998, Section 04

Gravetter, F. J., Wallnau, L. B. (1996). Statistics for the Behavioral Sciences:
A Kickoff Course for Students of Psychology and Education, 4th Edition. New York: West Publishing.

---

Chapter iv: Variability

So far we've discussed two of the 3 characteristics used to depict distributions, now we need to discuss the remaining - variability. Discover in our distributions that not every score is the same, e.g., non everybody gets the same score on the exam. So what we need to do is draw the varied results, rougly to describe the width of the distribution.

Variability provides a quantitiative measure of the degree to which scores in a distribution are spread out or clustered together.

In other words variablility refers to the caste of "differentness" of the scores in the distribution. High variability means that the scores differ past a lot, while low variability means that the scores are all similar ("homogeneousness").

We'll concentrate on iii measures of variability, the range , the interquartile range , and the standard deviation .

The simplest measure of variability is the range, which nosotros've already mentioned in our before discussions.

- The range is the divergence between the upper real limit of the largest (maximum) Ten value and the lower existent limit of the smallest (minimum) Ten value.

So look at your frequency distribution table, observe the highest and lowest scores and subtract the lowest from the highest (notation, if continuous must consider the existent limits).

__X f cf c% 10 2 25 100 9 viii 23 92 8 4 15 60 7 six eleven 44 6 4 v 20 5 1 i 4

if X is discrete then: the range = 10 - 5 = 5 if X is continuous and then: the range = ten.five- 4.5 = half-dozen

- there are some drawbacks of using the range as the description of the variability of a distribution

- the statistic is based solely on the two virtually extream values in the distribution, thus it doesn't capture all of the members of the distribution.

An culling measure of variability is the interquartile range.

So think back to percentiles. 50%tile equals the point at which exactly half the distribution exists on one side and the other half on the other side.

- Considering the same logic, what does the 25%tile represent? - The 75%?
- So using the 25th, 50th, & 75%tiles we tin can break the distribution into 4 quarters, or quartiles

_X f % c% 7 four 12.v 100 6 4 12.v 87.five 5 4 12.5 75 iv 8 25 62.5 iii four 12.5 37.v ii four 12.5 25 1 4 12.5 12.5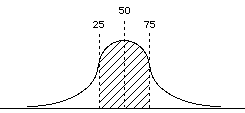

The interquartile range is the distance between the first quartile and the third quartile. Then this corresponds to the middle 50% of the scores of our distribution.

Then for the above distribution (assume that it is a continuous variable)

median = Q2 = 4.0 -> using interpolation (notice exactly halfway between 62.v & 37.5)
25%tile = Q1 = 2.five -> the upper existent limit for the interval 2
75%tile = Q3 = 5.5 -> the upper real limit for the interval 5

So the interquartile range (IQR) = 5.5 - 2.v = 3.0

Note that the interquartile range is often transformed into the semi-interquartile range which is 0.v of the interquartile range.

            SIQR =            (Q3 - Q1)            2          

So for our example the semi-interquartile range is (three.0)(0.5) = ane.five

So the interquartile range focusses on the centre half of all of the scores in the distribution. Thus it is more representative of the distribution equally a whole compared to the range and extreme scores (i.due east., outliers) will non influence the mensurate (sometimes refered to as being robust). Nonetheless, this nonetheless means that 1/two of the scores in the distribution are not represented in the measure.

The standard difference is the most pop and most important mensurate of variability. It takes into business relationship all of the individuals in the distribution.

In essence, the standard deviation measures how far off all of the individuals in the distribution are from a standard, where that standard is the mean of the distribution.

We will begin by discussion the standard deviation parameter, that is the standard departure of the population. Then nosotros will discuss the standard deviation statistic (for the sample). They are closely related descriptive statistics, but they accept some important differences.

So to go a measure out of the deviation we need to decrease the population mean from every individual in our distribution.

10 - m = deviation score
- if the score is a value above the hateful the deviation score volition be positive - if the score is a value below the mean the deviation score will be negative

Example: consider the following information set: the population of heights (in inches) for the class

69, 67, 72, 74, 63, 67, 64, 61, 69, 65, 70, 60, 75, 73, 63, 63, 69, 65, 64, 69, 65

hateful = m = 67

S (10 - g) = (69 - 67) + (67 - 67) + .... + (65 - 67) = ?
= 2+ 0 + 5 + vii + -iv + 0 + -3 + -half dozen + ii + -2 + iii + -7 + 8 + half dozen + -four + -4 + ii + -two + -3 + 2 + -ii
= 0

Find that if y'all add together up all of the deviations they should/must equal 0. Recall about it at a conceptual level. What you are doing is taking i side of the distribution and making it positive, and the other side negative and calculation them together. They should cancel each other out.

So what we accept to do is get rid of the negative signs. Nosotros do this by squaring the deviations and then taking the foursquare root of the sum of the squared deviations.

Sum of Squares = SS = S (Ten - chiliad)ⁱⁱ = (69 - 67) ² + (67 - 67) ⁱⁱ + .... + (65 - 67) ² =
SS = 4+ 0 + 25 + 49 + sixteen + 0 + 9 + 36 + 4 + 4 + ix +49 + 64 + 36 + sixteen + sixteen + 4 + iv + ix + iv + 4
SS = 362

The equation that we just used (SS = Due south (10 - g)²) is refered to as the definitional formula for the Sum of Squares. Yet, there is another way to compute the SS, refered to every bit the computational formula. The two equations are mathematically equivalent, however sometimes one is easier to utilise than the other. The reward of the computational formula is that it works with the Ten values directly.

The computational formula for SS is:

            SS =            SouthwardXii            -            (SX)            2            N

So for our example:

            SS = [(69)two            + (67)2            + ..... + (69)2            + (65)two] -            (69 + 67 + ... + 69 + 65)            2            21  	     =  94631  -            (1407)            2=  94631 - 94269  = 362 			    21

At present we have the sum of squares (SS), but to become the Population Variance which is simply the average of the squared deviations (we want the population variance non merely the SS, considering the SS depends on the number of individuals in the population, so we desire the mean). So to get the mean, we need to divide by the number of individuals in the population.

Population variance = s ² = SS/North

However the population variance isn't exactly what nosotros desire, nosotros desire the standard deviation from the mean of the population. To get this we need to have the square root of the population variance.

standard divergence = sqroot(variance) = sqroot(SS/North)

s = sqroot(south)

So for our example:

southward ² = 362 / 21 = 17.24
due south = sqroot (17.ii) = 4.fifteen

To review:

step 1: compute the SS

- either by using definitional formula or the computational formula

stride 2: determine the variance

- take the average of the squared deviations
- divide the SS by the North

footstep 3: make up one's mind the standard departure

- take the square root of the variance

Now permit'south move onto the Standard Deviation of a Sample

- the computations are pretty much the same here
- different note:
south = sample standard deviation
apply 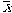instead of m in the computaion of SS

- need to suit the ciphering to tak into business relationship that a sample will typically be less variable than the respective population.



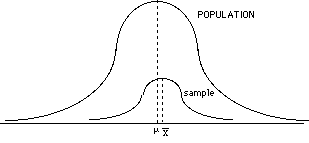
- if you take a good, representative sample, then your sample and population means should exist very similar, and the overall shape of the two distributions should be like. However, detect that the variability of the sample is smaller than the variability of the population.

- to account for this the sample variance is divided by n - 1 rather than simply n

                sample variance = s2                =                __SS _                n                - ane              

- and the same is truthful for sample standard difference

sample standard divergence = southward = sqroot(SS/(n - 1))
What we're really doing here is trying to employ a sample to make estimates almost the nature of the population. But since we don't know things like what is the hateful of the population, we actually can't measure our deviances from the population standard. Then what nosotros utilize is our all-time estimate of what the population mean is, and that is the sample mean.

So what nosotros're doing when we subtract 1 from n is using degrees of freedom to adjust our sample deviations to make an unbiased interpretation of the population values.

What are degrees of freedom? Think of information technology this way. You know what the sample mean is ahead of time (you've got to to figure out the deviations). So you tin can vary all just i item in the distribution. But the last item is fixed. There will be only 1 value for that item to brand the mean equal what it does. And so north - ane means all the values but one can vary.

Example:

suppose that yous know that the mean of your sample = 5
if your first 4 items are:
v, 4, 6, ii then what must the terminal number be?
5 + four + 6 + ii + X = 25
there volition exist only ane value of 10 that'll make this work. Ten = 8

Okay, and then allow's practice an example of calculating the standard deviation of a sample

data: ane, two, 3, 4, 4, five, 6, seven

footstep one: compute the SS

SS = S (10 - 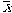)²
= (1 - 4)² + (two - 4)² + (3 - 4)² + (4 - 4)² + (4 - iv)² + (5 - four)² + (6 - 4)² + (7 - 4)²
= nine + 4 + 1 + 0 + 0 + 1 + iv + 9 = 28

-- OR --

You can nonetheless use the computational formula to become SS

                SS =                SX2                -                (S                  X)                two                N  		  = (1+4+9+16+sixteen+25+36+49) -                (1+2+three+iv+four+5+6+7)                8 		  = 156 - 128 = 28.0              

step 2: determine the variance of the sample (retrieve it is a sample, and so we need to have this into account)

                sample variance = sii                =                _SS_                n                - ane                
                  = 28/(8-ane) = 28/seven = 4.0                
              

footstep 3: determine the standard divergence of the sample
standard deviation = sqroot(SS/(n - 1))
= sqroot(28/(8 - 1)

= sqroot iv.0 = 2.0

Properties of the standard deviation (Transformations)

1) Adding a constant to each score in the distribution will not change the standard difference.

So if y'all add 2 to every score in the distribution, the mean changes (by 2), but the variance stays the same (notice that none of the deviations would alter because you add 2 to each score and the mean changes past 2).

ii) Multiplying each score by a constant causes the stardard deviation to be multiplied past the aforementioned constant.

This 1 is easier to call up of with numbers. Suppose that your mean is 20, and that two of the individuals in your distribution are 21 and 23. If y'all multiply 21 and 23 past two y'all get 42 and 46, and your mean too changes by a factor of 2 and is now 40. Before your deviations were (21 - 20 = i) & (23 - twenty = 3). Merely now, your deviations are (42 - xl = 2) & (46 - 40 = 6). So your deviations are getting twice as large likewise.

Comparison Measures of Variability

- Extreme scores: range is most afflicted, IQR is least affected
- Sample size: range tends to increase as n increases, IQR & south do not
- The range does not take stable values when you repeatedly sample from the aforementioned population, but the IQR & S are stable and tend not to fluctuate.
- With open-ended distributions, ane cannot even compute the range or S, so the IQR (or SIQR) is the only option

williamselithe66.blogspot.com

Source: https://psychology.illinoisstate.edu/jccutti/psych240/chpt4.html

Share this post